Coordinate surfaces of parabolic cylindrical coordinates. The red parabolic cylinder corresponds to σ=2, whereas the yellow parabolic cylinder corresponds to τ=1. The blue plane corresponds to z=2. These surfaces intersect at the point P (shown as a black sphere), which has Cartesian coordinates roughly (2, −1.5, 2).
In mathematics, parabolic cylindrical coordinates are a three-dimensional orthogonal coordinate system that results from projecting the two-dimensional parabolic coordinate system in the perpendicular z {\displaystyle z} -direction. Hence, the coordinate surfaces are confocal parabolic cylinders. Parabolic cylindrical coordinates he found many applications, e.g., the potential theory of edges.
Basic definition[edit]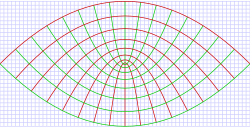
-direction. Hence, the coordinate surfaces are confocal parabolic cylinders. Parabolic cylindrical coordinates he found many applications, e.g., the potential theory of edges.
Parabolic coordinate system showing curves of constant σ and τ the horizontal and vertical axes are the x and y coordinates respectively. These coordinates are projected along the z-axis, and so this diagram will hold for any value of the z coordinate.
The parabolic cylindrical coordinates (σ, τ, z) are defined in terms of the Cartesian coordinates (x, y, z) by:
x = σ τ y = 1 2 ( τ 2 − σ 2 ) z = z {\displaystyle {\begin{aligned}x&=\sigma \tau \\y&={\frac {1}{2}}\left(\tau ^{2}-\sigma ^{2}\right)\\z&=z\end{aligned}}}
The surfaces of constant σ form confocal parabolic cylinders
2 y = x 2 σ 2 − σ 2 {\displaystyle 2y={\frac {x^{2}}{\sigma ^{2}}}-\sigma ^{2}}
that open towards +y, whereas the surfaces of constant τ form confocal parabolic cylinders
2 y = − x 2 τ 2 + τ 2 {\displaystyle 2y=-{\frac {x^{2}}{\tau ^{2}}}+\tau ^{2}}
that open in the opposite direction, i.e., towards −y. The foci of all these parabolic cylinders are located along the line defined by x = y = 0. The radius r has a simple formula as well
r = x 2 + y 2 = 1 2 ( σ 2 + τ 2 ) {\displaystyle r={\sqrt {x^{2}+y^{2}}}={\frac {1}{2}}\left(\sigma ^{2}+\tau ^{2}\right)}
that proves useful in solving the Hamilton–Jacobi equation in parabolic coordinates for the inverse-square central force problem of mechanics; for further details, see the Laplace–Runge–Lenz vector article.
Scale factors[edit]The scale factors for the parabolic cylindrical coordinates σ and τ are:
h σ = h τ = σ 2 + τ 2 h z = 1 {\displaystyle {\begin{aligned}h_{\sigma }&=h_{\tau }={\sqrt {\sigma ^{2}+\tau ^{2}}}\\h_{z}&=1\end{aligned}}} Differential elements[edit]
Differential elements[edit]
The infinitesimal element of volume is
d V = h σ h τ h z d σ d τ d z = ( σ 2 + τ 2 ) d σ d τ d z {\displaystyle dV=h_{\sigma }h_{\tau }h_{z}d\sigma d\tau dz=(\sigma ^{2}+\tau ^{2})d\sigma \,d\tau \,dz}
The differential displacement is given by:
d l = σ 2 + τ 2 d σ σ ^ + σ 2 + τ 2 d τ τ ^ + d z z ^ {\displaystyle d\mathbf {l} ={\sqrt {\sigma ^{2}+\tau ^{2}}}\,d\sigma \,{\boldsymbol {\hat {\sigma }}}+{\sqrt {\sigma ^{2}+\tau ^{2}}}\,d\tau \,{\boldsymbol {\hat {\tau }}}+dz\,\mathbf {\hat {z}} }
The differential normal area is given by:
d S = σ 2 + τ 2 d τ d z σ ^ + σ 2 + τ 2 d σ d z τ ^ + ( σ 2 + τ 2 ) d σ d τ z ^ {\displaystyle d\mathbf {S} ={\sqrt {\sigma ^{2}+\tau ^{2}}}\,d\tau \,dz{\boldsymbol {\hat {\sigma }}}+{\sqrt {\sigma ^{2}+\tau ^{2}}}\,d\sigma \,dz{\boldsymbol {\hat {\tau }}}+\left(\sigma ^{2}+\tau ^{2}\right)\,d\sigma \,d\tau \mathbf {\hat {z}} } Del[edit]
Del[edit]
Let f be a scalar field. The gradient is given by
∇ f = 1 σ 2 + τ 2 ∂ f ∂ σ σ ^ + 1 σ 2 + τ 2 ∂ f ∂ τ τ ^ + ∂ f ∂ z z ^ {\displaystyle \nabla f={\frac {1}{\sqrt {\sigma ^{2}+\tau ^{2}}}}{\partial f \over \partial \sigma }{\boldsymbol {\hat {\sigma }}}+{\frac {1}{\sqrt {\sigma ^{2}+\tau ^{2}}}}{\partial f \over \partial \tau }{\boldsymbol {\hat {\tau }}}+{\partial f \over \partial z}\mathbf {\hat {z}} }
The Laplacian is given by
∇ 2 f = 1 σ 2 + τ 2 ( ∂ 2 f ∂ σ 2 + ∂ 2 f ∂ τ 2 ) + ∂ 2 f ∂ z 2 {\displaystyle \nabla ^{2}f={\frac {1}{\sigma ^{2}+\tau ^{2}}}\left({\frac {\partial ^{2}f}{\partial \sigma ^{2}}}+{\frac {\partial ^{2}f}{\partial \tau ^{2}}}\right)+{\frac {\partial ^{2}f}{\partial z^{2}}}}
Let A be a vector field of the form:
A = A σ σ ^ + A τ τ ^ + A z z ^ {\displaystyle \mathbf {A} =A_{\sigma }{\boldsymbol {\hat {\sigma }}}+A_{\tau }{\boldsymbol {\hat {\tau }}}+A_{z}\mathbf {\hat {z}} }
The divergence is given by
∇ ⋅ A = 1 σ 2 + τ 2 ( ∂ ( σ 2 + τ 2 A σ ) ∂ σ + ∂ ( σ 2 + τ 2 A τ ) ∂ τ ) + ∂ A z ∂ z {\displaystyle \nabla \cdot \mathbf {A} ={\frac {1}{\sigma ^{2}+\tau ^{2}}}\left({\partial ({\sqrt {\sigma ^{2}+\tau ^{2}}}A_{\sigma }) \over \partial \sigma }+{\partial ({\sqrt {\sigma ^{2}+\tau ^{2}}}A_{\tau }) \over \partial \tau }\right)+{\partial A_{z} \over \partial z}}
The curl is given by
∇ × A = ( 1 σ 2 + τ 2 ∂ A z ∂ τ − ∂ A τ ∂ z ) σ ^ − ( 1 σ 2 + τ 2 ∂ A z ∂ σ − ∂ A σ ∂ z ) τ ^ + 1 σ 2 + τ 2 ( ∂ ( σ 2 + τ 2 A τ ) ∂ σ − ∂ ( σ 2 + τ 2 A σ ) ∂ τ ) z ^ {\displaystyle \nabla \times \mathbf {A} =\left({\frac {1}{\sqrt {\sigma ^{2}+\tau ^{2}}}}{\frac {\partial A_{z}}{\partial \tau }}-{\frac {\partial A_{\tau }}{\partial z}}\right){\boldsymbol {\hat {\sigma }}}-\left({\frac {1}{\sqrt {\sigma ^{2}+\tau ^{2}}}}{\frac {\partial A_{z}}{\partial \sigma }}-{\frac {\partial A_{\sigma }}{\partial z}}\right){\boldsymbol {\hat {\tau }}}+{\frac {1}{\sigma ^{2}+\tau ^{2}}}\left({\frac {\partial \left({\sqrt {\sigma ^{2}+\tau ^{2}}}A_{\tau }\right)}{\partial \sigma }}-{\frac {\partial \left({\sqrt {\sigma ^{2}+\tau ^{2}}}A_{\sigma }\right)}{\partial \tau }}\right)\mathbf {\hat {z}} }
Other differential operators can be expressed in the coordinates (σ, τ) by substituting the scale factors into the general formulae found in orthogonal coordinates.
Relationship to other coordinate systems[edit]Relationship to cylindrical coordinates (ρ, φ, z):
ρ cos φ = σ τ ρ sin φ = 1 2 ( τ 2 − σ 2 ) z = z {\displaystyle {\begin{aligned}\rho \cos \varphi &=\sigma \tau \\\rho \sin \varphi &={\frac {1}{2}}\left(\tau ^{2}-\sigma ^{2}\right)\\z&=z\end{aligned}}}
Parabolic unit vectors expressed in terms of Cartesian unit vectors:
σ ^ = τ x ^ − σ y ^ τ 2 + σ 2 τ ^ = σ x ^ + τ y ^ τ 2 + σ 2 z ^ = z ^ {\displaystyle {\begin{aligned}{\boldsymbol {\hat {\sigma }}}&={\frac {\tau {\hat {\mathbf {x} }}-\sigma {\hat {\mathbf {y} }}}{\sqrt {\tau ^{2}+\sigma ^{2}}}}\\{\boldsymbol {\hat {\tau }}}&={\frac {\sigma {\hat {\mathbf {x} }}+\tau {\hat {\mathbf {y} }}}{\sqrt {\tau ^{2}+\sigma ^{2}}}}\\\mathbf {\hat {z}} &=\mathbf {\hat {z}} \end{aligned}}} Parabolic cylinder harmonics[edit]
Parabolic cylinder harmonics[edit]
Since all of the surfaces of constant σ, τ and z are conicoids, Laplace's equation is separable in parabolic cylindrical coordinates. Using the technique of the separation of variables, a separated solution to Laplace's equation may be written:
V = S ( σ ) T ( τ ) Z ( z ) {\displaystyle V=S(\sigma )T(\tau )Z(z)}
and Laplace's equation, divided by V, is written:
1 σ 2 + τ 2 [ S ¨ S + T ¨ T ] + Z ¨ Z = 0 {\displaystyle {\frac {1}{\sigma ^{2}+\tau ^{2}}}\left[{\frac {\ddot {S}}{S}}+{\frac {\ddot {T}}{T}}\right]+{\frac {\ddot {Z}}{Z}}=0}![{\displaystyle {\frac {1}{\sigma ^{2}+\tau ^{2}}}\left[{\frac {\ddot {S}}{S}}+{\frac {\ddot {T}}{T}}\right]+{\frac {\ddot {Z}}{Z}}=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/99190e6afe07d230b871dd5a2f159b9cf8179d2c)
Since the Z equation is separate from the rest, we may write
Z ¨ Z = − m 2 {\displaystyle {\frac {\ddot {Z}}{Z}}=-m^{2}}
where m is constant. Z(z) has the solution:
Z m ( z ) = A 1 e i m z + A 2 e − i m z {\displaystyle Z_{m}(z)=A_{1}\,e^{imz}+A_{2}\,e^{-imz}}
Substituting −m2 for Z ¨ / Z {\displaystyle {\ddot {Z}}/Z} , Laplace's equation may now be written:
[ S ¨ S + T ¨ T ] = m 2 ( σ 2 + τ 2 ) {\displaystyle \left[{\frac {\ddot {S}}{S}}+{\frac {\ddot {T}}{T}}\right]=m^{2}(\sigma ^{2}+\tau ^{2})}
, Laplace's equation may now be written:
![{\displaystyle \left[{\frac {\ddot {S}}{S}}+{\frac {\ddot {T}}{T}}\right]=m^{2}(\sigma ^{2}+\tau ^{2})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/544c991ae2342d2a4f196e566d4357f7195a7c6c)
We may now separate the S and T functions and introduce another constant n2 to obtain:
S ¨ − ( m 2 σ 2 + n 2 ) S = 0 {\displaystyle {\ddot {S}}-(m^{2}\sigma ^{2}+n^{2})S=0} T ¨ − ( m 2 τ 2 − n 2 ) T = 0 {\displaystyle {\ddot {T}}-(m^{2}\tau ^{2}-n^{2})T=0}
T
¨
−
(
m
2
τ
2
−
n
2
)
T
=
0
{\displaystyle {\ddot {T}}-(m^{2}\tau ^{2}-n^{2})T=0}
The solutions to these equations are the parabolic cylinder functions
S m n ( σ ) = A 3 y 1 ( n 2 / 2 m , σ 2 m ) + A 4 y 2 ( n 2 / 2 m , σ 2 m ) {\displaystyle S_{mn}(\sigma )=A_{3}y_{1}(n^{2}/2m,\sigma {\sqrt {2m}})+A_{4}y_{2}(n^{2}/2m,\sigma {\sqrt {2m}})} T m n ( τ ) = A 5 y 1 ( n 2 / 2 m , i τ 2 m ) + A 6 y 2 ( n 2 / 2 m , i τ 2 m ) {\displaystyle T_{mn}(\tau )=A_{5}y_{1}(n^{2}/2m,i\tau {\sqrt {2m}})+A_{6}y_{2}(n^{2}/2m,i\tau {\sqrt {2m}})}
T
m
n
(
τ
)
=
A
5
y
1
(
n
2
/
2
m
,
i
τ
2
m
)
+
A
6
y
2
(
n
2
/
2
m
,
i
τ
2
m
)
{\displaystyle T_{mn}(\tau )=A_{5}y_{1}(n^{2}/2m,i\tau {\sqrt {2m}})+A_{6}y_{2}(n^{2}/2m,i\tau {\sqrt {2m}})}
The parabolic cylinder harmonics for (m, n) are now the product of the solutions. The combination will reduce the number of constants and the general solution to Laplace's equation may be written:
V ( σ , τ , z ) = ∑ m , n A m n S m n T m n Z m {\displaystyle V(\sigma ,\tau ,z)=\sum _{m,n}A_{mn}S_{mn}T_{mn}Z_{m}} Applications[edit]
Applications[edit]
The classic applications of parabolic cylindrical coordinates are in solving partial differential equations, e.g., Laplace's equation or the Helmholtz equation, for which such coordinates allow a separation of variables. A typical example would be the electric field surrounding a flat semi-infinite conducting plate.
See also[edit] Parabolic coordinates Orthogonal coordinate system Curvilinear coordinates Bibliography[edit] Morse PM, Feshbach H (1953). Methods of Theoretical Physics, Part I. New York: McGraw-Hill. p. 658. ISBN 0-07-043316-X. LCCN 52011515. {{cite book}}: ISBN / Date incompatibility (help) Margenau H, Murphy GM (1956). The Mathematics of Physics and Chemistry. New York: D. van Nostrand. pp. 186–187. LCCN 55010911. Korn GA, Korn TM (1961). Mathematical Handbook for Scientists and Engineers. New York: McGraw-Hill. p. 181. LCCN 59014456. ASIN B0000CKZX7. Sauer R, Szabó I (1967). Mathematische Hilfsmittel des Ingenieurs. New York: Springer Verlag. p. 96. LCCN 67025285. Zwillinger D (1992). Handbook of Integration. Boston, MA: Jones and Bartlett. p. 114. ISBN 0-86720-293-9. Same as Morse & Feshbach (1953), substituting uk for ξk. Moon P, Spencer DE (1988). "Parabolic-Cylinder Coordinates (μ, ν, z)". Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions (corrected 2nd ed., 3rd print ed.). New York: Springer-Verlag. pp. 21–24 (Table 1.04). ISBN 978-0-387-18430-2. External links[edit] MathWorld description of parabolic cylindrical coordinates vteOrthogonal coordinate systemsTwo dimensional Cartesian Polar (Log-polar) Parabolic Bipolar Elliptic Three dimensional Cartesian Cylindrical Spherical Parabolic Paraboloidal Oblate spheroidal Prolate spheroidal Ellipsoidal Elliptic cylindrical Toroidal Bispherical Bipolar cylindrical Conical 6-sphere