This is a short list of some common mathematical shapes and figures and the formulas that describe them.
Two-dimensional shapes[edit] Shape Area Perimeter/Circumference Meanings of symbols Square l 2 {\displaystyle l^{2}} 4 l {\displaystyle 4l} l {\displaystyle l} is the length of a side Rectangle l b {\displaystyle lb} 2 ( l + b ) {\displaystyle 2(l+b)} l {\displaystyle l} is length, b {\displaystyle b} is breadth Circle π r 2 {\displaystyle \pi r^{2}} 2 π r {\displaystyle 2\pi r} or π d {\displaystyle \pi d} where r {\displaystyle r} is the radius and d {\displaystyle d} is the diameter Ellipse π a b {\displaystyle \pi ab} where a {\displaystyle a} is the semimajor axis and b {\displaystyle b} is the semiminor axis Triangle b h 2 {\displaystyle {\frac {bh}{2}}} a + b + c {\displaystyle a+b+c} b {\displaystyle b} is base; h {\displaystyle h} is height; a , b , c {\displaystyle a,b,c} are sides Parallelogram b h {\displaystyle bh} 2 ( a + b ) {\displaystyle 2(a+b)} b {\displaystyle b} is base, h {\displaystyle h} is height, a {\displaystyle a} is side Trapezoid a + b 2 h {\displaystyle {\frac {a+b}{2}}h} a {\displaystyle a} and b {\displaystyle b} are the bases Sources:[1][2][3] Three-dimensional shapes[edit] Illustration of the shapes' equation terms
4
l
{\displaystyle 4l}
l
{\displaystyle l}
is the length of a side
Rectangle
l
b
{\displaystyle lb}
2
(
l
+
b
)
{\displaystyle 2(l+b)}
l
{\displaystyle l}
is breadth
Circle
π
r
2
{\displaystyle \pi r^{2}}
2
π
r
{\displaystyle 2\pi r}
or
π
d
{\displaystyle \pi d}
where
r
{\displaystyle r}
is the radius and
d
{\displaystyle d}
is the diameter
Ellipse
π
a
b
{\displaystyle \pi ab}
where
a
{\displaystyle a}
is the semimajor axis and
b
{\displaystyle b}
a
+
b
+
c
{\displaystyle a+b+c}
b
{\displaystyle b}
is height;
a
,
b
,
c
{\displaystyle a,b,c}
are sides
Parallelogram
b
h
{\displaystyle bh}
2
(
a
+
b
)
{\displaystyle 2(a+b)}
b
{\displaystyle b}
a
{\displaystyle a}
Cube
Cuboid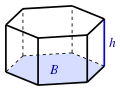
Prism
Parallelepiped
Pyramids
Tetrahedron
Cone
Cylinder
Sphere
Ellipsoid
This is a list of volume formulas of basic shapes:[4]: 405–406
Cone – 1 3 π r 2 h {\textstyle {\frac {1}{3}}\pi r^{2}h} , where r {\textstyle r} is the base's radius and h {\textstyle h} is the cone's height; Cube – a 3 {\textstyle a^{3}} , where a {\textstyle a} is the side's length; Cuboid – a b c {\textstyle abc} , where a {\textstyle a} , b {\textstyle b} , and c {\textstyle c} are the sides' length; Cylinder – π r 2 h {\textstyle \pi r^{2}h} , where r {\textstyle r} is the base's radius and h {\textstyle h} is the cylinder's height; Ellipsoid – 4 3 π a b c {\textstyle {\frac {4}{3}}\pi abc} , where a {\textstyle a} , b {\textstyle b} , and c {\textstyle c} are the semi-major and semi-minor axes' length; Sphere – 4 3 π r 3 {\textstyle {\frac {4}{3}}\pi r^{3}} , where r {\textstyle r} is the radius; Parallelepiped – a b c K {\textstyle abc{\sqrt {K}}} , where a {\textstyle a} , b {\textstyle b} , and c {\textstyle c} are the sides' length, K = 1 + 2 cos ( α ) cos ( β ) cos ( γ ) − cos 2 ( α ) − cos 2 ( β ) − cos 2 ( γ ) {\textstyle K=1+2\cos(\alpha )\cos(\beta )\cos(\gamma )-\cos ^{2}(\alpha )-\cos ^{2}(\beta )-\cos ^{2}(\gamma )} , and α {\textstyle \alpha } , β {\textstyle \beta } , and γ {\textstyle \gamma } are angles between the two sides; Prism – B h {\textstyle Bh} , where B {\textstyle B} is the base's area and h {\textstyle h} is the prism's height; Pyramid – 1 3 B h {\textstyle {\frac {1}{3}}Bh} , where B {\textstyle B} is the base's area and h {\textstyle h} is the pyramid's height; Tetrahedron – 2 12 a 3 {\textstyle {{\sqrt {2}} \over 12}a^{3}} , where a {\textstyle a} is the side's length. Sphere[edit] See also: Volume of an n-ball and n-sphere § Volume and surface area
, where
r
{\textstyle r}
is the base's radius and
h
{\textstyle h}
is the cone's height;
Cube –
a
3
{\textstyle a^{3}}
, where
a
{\textstyle a}
is the side's length;
Cuboid –
a
b
c
{\textstyle abc}
, where
a
{\textstyle a}
, and
c
{\textstyle c}
are the sides' length;
Cylinder –
π
r
2
h
{\textstyle \pi r^{2}h}
, where
r
{\textstyle r}
, where
a
{\textstyle a}
, where
r
{\textstyle r}
, where
a
{\textstyle a}
, and
α
{\textstyle \alpha }
,
β
{\textstyle \beta }
, and
γ
{\textstyle \gamma }
are angles between the two sides;
Prism –
B
h
{\textstyle Bh}
, where
B
{\textstyle B}
is the base's area and
h
{\textstyle h}
, where
B
{\textstyle B}
, where
a
{\textstyle a}
The basic quantities describing a sphere (meaning a 2-sphere, a 2-dimensional surface inside 3-dimensional space) will be denoted by the following variables
r {\displaystyle r} is the radius, C = 2 π r {\displaystyle C=2\pi r} is the circumference (the length of any one of its great circles), S {\displaystyle S} is the surface area, V {\displaystyle V} is the volume.
is the circumference (the length of any one of its great circles),
S
{\displaystyle S}
is the surface area,
V
{\displaystyle V}
is the volume.
Surface area:
S = 4 π r 2 = 1 π C 2 = π ( 6 V ) 2 3 {\displaystyle {\begin{alignedat}{4}S&=4\pi r^{2}\\[0.3ex]&={\frac {1}{\pi }}C^{2}\\[0.3ex]&={\sqrt[{3}]{\pi (6V)^{2}}}\\[0.3ex]\end{alignedat}}}
![{\displaystyle {\begin{alignedat}{4}S&=4\pi r^{2}\\[0.3ex]&={\frac {1}{\pi }}C^{2}\\[0.3ex]&={\sqrt[{3}]{\pi (6V)^{2}}}\\[0.3ex]\end{alignedat}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3343b2b8dee9d19598b3d22afd243282f5ba9258)
Volume:
V = 4 3 π r 3 = 1 6 π 2 C 3 = 1 6 π S 3 / 2 {\displaystyle {\begin{alignedat}{4}V&={\frac {4}{3}}\pi r^{3}\\[0.3ex]&={\frac {1}{6\pi ^{2}}}C^{3}\\[0.3ex]&={\frac {1}{6{\sqrt {\pi }}}}S^{3/2}\\[0.3ex]\end{alignedat}}}
![{\displaystyle {\begin{alignedat}{4}V&={\frac {4}{3}}\pi r^{3}\\[0.3ex]&={\frac {1}{6\pi ^{2}}}C^{3}\\[0.3ex]&={\frac {1}{6{\sqrt {\pi }}}}S^{3/2}\\[0.3ex]\end{alignedat}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4a55292a264b71a1c93c0029661c27c103d36fb)
Radius:
r = 1 2 π C = 1 4 π S = 3 4 π V 3 {\displaystyle {\begin{alignedat}{4}r&={\frac {1}{2\pi }}C\\[0.3ex]&={\sqrt {{\frac {1}{4\pi }}S}}\\[0.3ex]&={\sqrt[{3}]{{\frac {3}{4\pi }}V}}\\[0.3ex]\end{alignedat}}}
![{\displaystyle {\begin{alignedat}{4}r&={\frac {1}{2\pi }}C\\[0.3ex]&={\sqrt {{\frac {1}{4\pi }}S}}\\[0.3ex]&={\sqrt[{3}]{{\frac {3}{4\pi }}V}}\\[0.3ex]\end{alignedat}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44148d0c75e7d25e2a81126a79cade3e76c3085e)
Circumference:
C = 2 π r = π S = π 2 6 V 3 {\displaystyle {\begin{alignedat}{4}C&=2\pi r\\[0.3ex]&={\sqrt {\pi S}}\\[0.3ex]&={\sqrt[{3}]{\pi ^{2}6V}}\\[0.3ex]\end{alignedat}}}
See also[edit] Arc length – Distance along a curve Area#Area formulas – Size of a two-dimensional surface Perimeter#Formulas – Path that surrounds an area List of second moments of area List of surface-area-to-volume ratios – Surface area per unit volume List of surface area formulas – Measure of a two-dimensional surface List of trigonometric identities List of volume formulas – Quantity of three-dimensional space References[edit] ^ "Archived copy" (PDF). Archived from the original (PDF) on 2012-08-13. Retrieved 2011-11-29.{{cite web}}: CS1 maint: archived copy as title (link) ^ "Area Formulas". ^ "List of Basic Geometry Formulas". 27 May 2018. ^ Treese, Steven A. (2018). History and Measurement of the Base and Derived Units. Cham, Switzerland: Springer Science+Business Media. ISBN 978-3-319-77577-7. LCCN 2018940415. OCLC 1036766223.![{\displaystyle {\begin{alignedat}{4}C&=2\pi r\\[0.3ex]&={\sqrt {\pi S}}\\[0.3ex]&={\sqrt[{3}]{\pi ^{2}6V}}\\[0.3ex]\end{alignedat}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33f6840e1d98b85ab9336df84dbcbf61b3e03158)