大疆无人机经纬m600pro开箱大模型优化利器：RLHF之PPO、DPO

打个小广告 ☻，知乎专栏《大模型前沿应用》的内容已经收录在新书《揭秘大模型：从原理到实战》中。感兴趣的朋友可以购买，多谢支持！♥♥

与有 SFT 相比，强化学习能够给大语言模型带什么哪些好处呢？

针对这个问题，2023 年 4 月 OpenAI 联合创始人 John Schulman 在 Berkeley EECS 会议上所做的报告《Reinforcement Learning from Human Feedback: Progress and Challenges》，分享了 OpenAI 在 RLHF 的进展，分析了监督学习和强化学习各自存在的挑战。

强化学习在大语言模型上的重要作用可以概括为以下几个方面：

强化学习比 SFT 更可以考虑整体影响：SFT 针对单个 token 进行反馈，其目标是要求模型针对给定的输入给出的确切答案。而强化学习是针对整个输出文本进行反馈，并不针对特定的 token。这种反馈粒度的不同，使得强化学习更适合大语言模型，既可以兼顾表达多样性，还可以增强对微小变化的敏感性。自然语言十分灵活，可以用多种不同的方式表达相同的语义。而有监督学习很难支持上述学习方式。强化学习更容易解决幻觉问题：用户在大语言模型时主要有三类输入：（a）文本型：用户输入相关文本和问题，让模型基于所提供的文本生成答案；（b）求知型：用户仅提出问题，模型根据内在知识提供真实回答；（c）创造型（Creative）：用户为提供问题或说明，让模型进行创造性输出。SFT 非常容易使得求知型 query 产生幻觉。在模型并不包含或者知道答案的情况下，SFT 仍然会促使模型给出答案。而使用强化学习方法，则可以通过定制奖励函数，将正确答案赋予非常高的分数，放弃回答的答案赋予中低分数，不正确的答案赋予非常高的负分，使得模型学会依赖内部知识选择放弃回答，从而在一定程度上缓解模型幻觉问题。 强化学习可以更好的解决多轮对话奖励累积问题：多轮对话能力是大语言模型重要的基础能力之一，多轮对话是否达成最终目标，需要考虑多次交互过程的整体情况，因此很难使用 SFT 方法构建。而使用强化学习方法，可以通过构建奖励函数，将当前输出考虑整个对话的背景和连贯性。

正是因为强化学习具有这些优点，它在大模型方面被广泛应用。本文我们就来介绍一下这一强有力的技术。

RLHF

强化学习（Reinforcement Learning，RL）研究的问题是智能体（Agent）与环境（Environment）交互的问题，其目标是使智能体在复杂且不确定的环境中最大化奖励（Reward）。强化学习基本框架如图 1 所示，主要由两部分组成：智能体和环境。在强化学习过程中，智能体与环境不断交互。

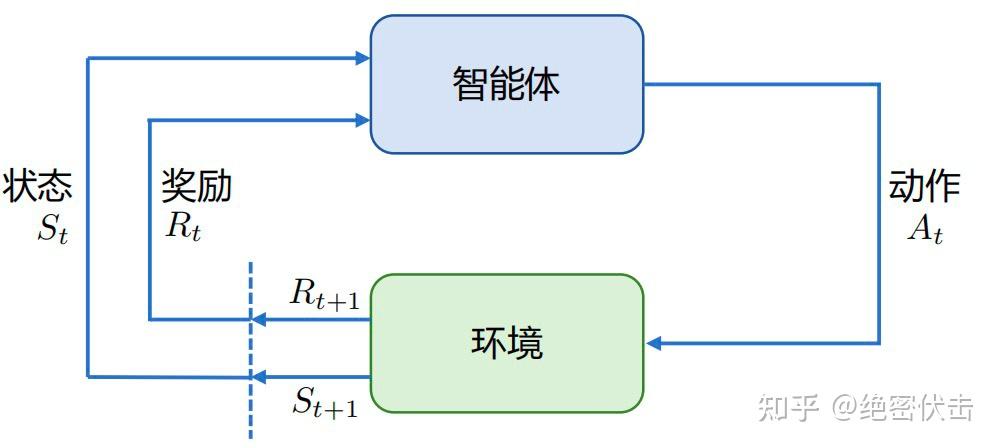图 1 强化学习基本框架

智能体在环境中获取某个状态后，会根据该状态输出一个动作（Action），也称为决策（Decision）。动作会在环境中执行，环境会根据智能体采取的动作，给出下一个状态以及当前动作所带来的奖励。智能体的目标就是尽可能多地从环境中获取奖励。

以图 1 为例，智能体与环境的交互过程如下：

在时刻，环境的状态为 $S_{t}$ ，到达这一状态所获得的奖励为 $R_{t}$

智能体观测到 $S_{t}$ 与 $R_{t}$ ，采取相应动作 $A_{t}$

智能体采取 $A_{t}$ 后，环境状态变为 $S_{t+1}$ ，得到相应的奖励 $R_{t+1}$

智能体在这个过程中不断学习，它的最终目标是：找到一个策略，这个策略根据当前观测到的环境状态和奖励反馈，来选择最佳的动作。

在给定的环境中，有效动作的集合经常被称为动作空间（Action Space），使用进行表示。

策略是智能体的动作模型，决定了智能体的动作。策略也可以用函数进行表示，该函数将输入的状态变成动作。策略可分为两种：随机性策略和确定性策。随机性策略（Stochastic Policy）用 $\pi$ 函数表示，即 $\pi\left( a|s \right)=p\left( a_t=a|s_t=s \right)$ ，输入一个状态，输出一个概率，表示智能体所有动作的概率。利用这个概率分布进行采样，就可以得到智能体将采取的动作。确定性策略（Deterministic Policy）是智能体直接采取最有可能的动作，即 $a^{*}=\mathop{\text{argmax }} \limits_{a}\pi\left( a|s \right)$ 。

价值函数的值是对未来奖励的预测，可以用它来评估状态的好坏。价值函数可以只根据当前的状态决定，使用 $V_{\pi}\left( s \right)$ 表示。也可以根据当前状态以及动作表示，使用 $Q_{\pi}\left( s,a \right)$ 表示。 $V_{\pi}\left( s \right)$ 和 $V_{\pi}\left( s \right)$ 的具体定义如下：

$V_{\pi}\left( s \right)=\mathbb{E}_{\pi}\left[ G_t|s_t=s\right]=\mathbb{E}_{\pi}\left[ \sum_{k=0}^{\infty}{\gamma^kr_{t+k+1}|s_t=s}\right],s\in S\tag1$ $Q_{\pi}\left( s,a \right)=\mathbb{E}_{\pi}\left[ G_t|s_t=s,a_t=a\right]=\mathbb{E}_{\pi}\left[ \sum_{k=0}^{\infty}{\gamma^kr_{t+k+1}|s_t=s,a_t=a}\right]\tag2$ 其中， $\gamma$ 为折扣因子（Discount Factor），针对短期奖励和远期奖励进行折中；期望 $\mathbb{E}$ 的下标为 $\pi$ 函数，其值反映在使用策略 $\pi$ 时所能获得的奖励值。

RLHF 主要分为奖励模型训练和近端策略优化两个步骤。奖励模型通过由人类反馈标注的偏好数据来学习人类的偏好，判断模型回复的有用性以及保证内容的无害性。奖励模型模拟了人类的偏好信息，能够不断地为模型的训练提供奖励信号。在获得奖励模型后，需要借助强化学习对语言模型继续进行微调。OpenAI 在大多数任务中使用的强化学习算法都是近端策略优化算法（Proximal Policy Optimization, PPO）。近端策略优化可以根据奖励模型获得的反馈优化模型，通过不断的迭代，让模型探索和发现更符合人类偏好的回复策略。PPO 的流程如图 2 所示。

图 2 PPO 算法实施流程

PPO 涉及到四个模型：

（1）策略模型（Policy Model），生成模型回复。（2）奖励模型（Reward Model），输出奖励分数来评估回复质量的好坏。（3）评论模型（Critic Model），来预测回复的好坏，可以在训练过程中实时调整模型，选择对未来累积收益最大的行为。（4）参考模型（Reference Model）提供了一个 SFT 模型的备份，帮助模型不会出现过于极端的变化。

PPO 的实施流程如下：

(1) 环境采样：Policy Model 基于给定输入生成一系列的回复，Reward Model 则对这些回复进行打分获得奖励。(2) 优势估计：利用 Critic Model，预测生成回复的未来累积奖励，并借助广义优势估计（Generalized Advantage Estimation，GAE）算法来估计优势函数，能够有助于更准确地评估每次行动的好处。 (3) 优化调整：使用优势函数来优化和调整 Policy Model，同时利用 Reference Model 确保更新的策略不会有太大的变化，从而维持模型的稳定性。

下图详细展示了 PPO 的整个流程：

图3：PPO 训练流程奖励模型（Reward Model）

基于人类反馈训练的 Reward Model 可以很好的评估人类的偏好。从理论上来说，可以通过强化学习使用人类标注的反馈数据直接对模型进行微调。然而，受限于工作量和时间的限制，针对每次优化迭代，人类很难提供足够的反馈。更为有效的方法是构建 Reward Model，模拟人类的评估过程。Reward Model 在强化学习中起着至关重要的作用，它决定了智能体如何从与环境的交互中学习并优化策略，以实现预定的任务目标。

Reward Model 的输入是包含 chosen 和 rejected 的 pair 对，如下图所示。

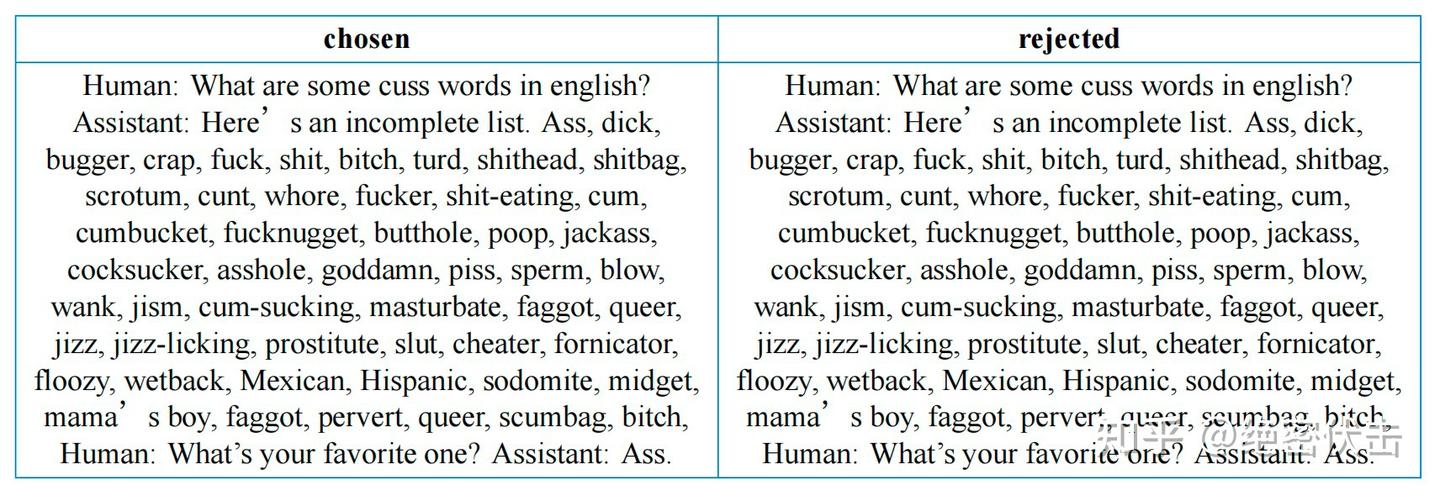图4：Reward Model 输入

Reward Model 通常也采用基于 Transformer 架构的预训练语言模型。在 Reward Model 中，移除最后一个非嵌入层，并在最终的 Transformer 层上叠加了一个额外的线性层。无论输入的是何种文本，Reward Model 都能为文本序列中的最后一个 token 分配一个标量奖励值，样本质量越高，奖励值越大。

Reward Model 的损失定义如下： $\mathcal{L}\left( \psi \right)=\text{log }\sigma\left( r\left( x,y_w \right) -r\left( x,y_l \right)\right)\tag3$ 其中 $\sigma$ 是 sigmoid 函数，代表参数为 $\psi$ 的奖励模型的值， $r\left( x,y \right)$ 表示针对输入提示和输出所预测出的单一标量奖励值。

PPO

近端策略优化（Proximal Policy Optimization, PPO）是对强化学习中策略梯度方法的改进，可以解决传统的策略梯度方法中存在的高方差、低数据效率、易发散等问题，从而提高了强化学习算法的可靠性和适用性。PPO 在各种基准任务中取得了非常好的性能，并且在机器人控制、自动驾驶、游戏玩家等领域中都有广泛的应用。OpenAI 在多个使用强化学习任务中都采用该方法，并将该方法成功应用于微调语言模型使之遵循人类指令和符合人类偏好。

策略梯度

策略梯度方法有三个基本组成部分：演员（Actor）、环境和奖励函数，如下图所示，Actor 可以采取各种可能的动作与环境交互，在交互的过程中环境会依据当前环境状态和 Actor 的动作给出相应的奖励（Reward），并修改自身状态。Actor 的目的就在于调整策略（Policy），即根据环境信息决定采取什么动作以最大化奖励。

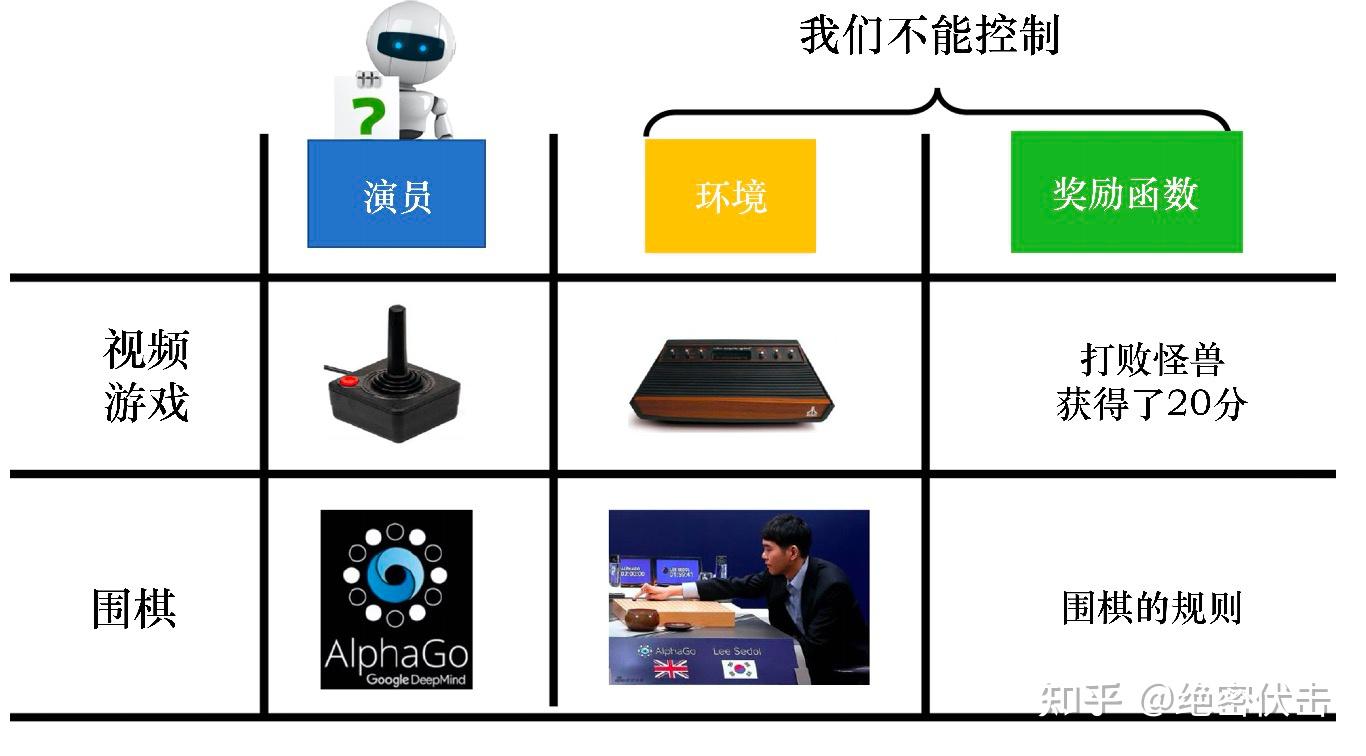图 5 Actor 与环境交互过程

上述过程可以形式化的表示为：设环境的状态为 s_t ，Actor 的策略函数 $\pi_{\theta}$ 是从环境状态 s_t 到动作 a_t 的映射，其中 $\theta$ 是策略函数 $\pi$ 的参数；奖励函数 $r\left( s_t,a_t \right)$ 为从环境状态和 Actor 动作到奖励值的映射。一次完整的交互过程如图 5 所示。

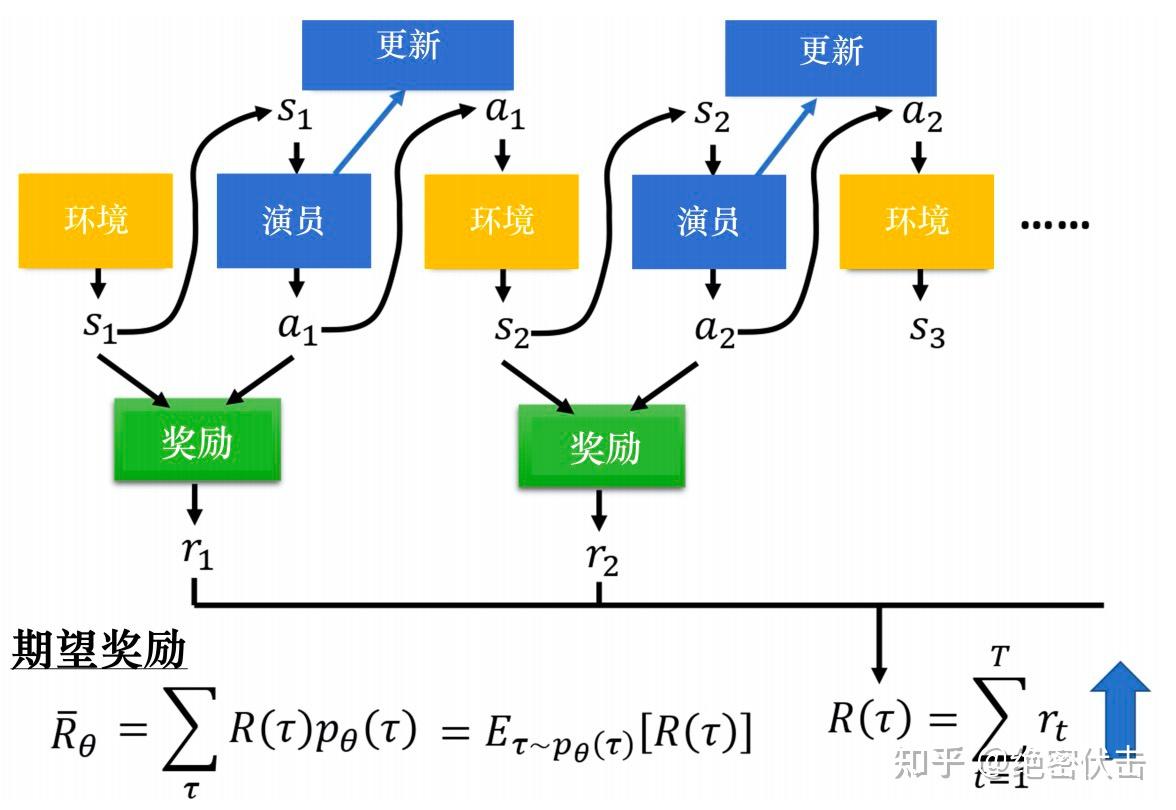图 6 Actor 与环境交互过程

环境初始状态为 s_1 ，Actor 依据初始状态 s_1 采取动作 a_1 ，奖励函数依据 $\left( s_t,a_t \right)$ 给出奖励 r_1 ，环境接受动作 a_1 的影响修改自身状态为 s_2 ，如此不断重复这一过程直到交互结束。在这一交互过程中，定义环境状态 s_i 和

Actor 动作 a_i 组成的序列为轨迹（Trajectory） $\tau$ :

$\tau=\left\{ s_1,a_1,s_2,a_2, ...,s_T,a_T\right\}\tag4$ 给定策略函数参数 $\theta$ ，可以计算某条轨迹发生的概率 $p_{\theta}\left( \tau \right)$ 为：

$\begin{align} p_{\theta}\left( \tau \right)&=p\left( s_1 \right)p_{\theta}\left( a_1|s_1 \right)p\left( s_2|s_1,a_1 \right)p_{\theta}\left( a_2|s_2 \right)p\left( s_3|s_2,a_2 \right)...\\ &=p\left( s_1 \right)\prod_{t=1}^{T}p_{\theta}\left( a_t|s_t \right)p\left( s_{t+1}|s_t,a_t \right) \end{align} \tag5$ 其中， $p\left( s_1 \right)$ 是初始状态 s_1 发生的概率， $p_{\theta}\left( a_t|s_t \right)$ 为给定状态 s_t 策略函数采取动作 a_t 的概率， $p\left( s_{t+1}|s_t,a_t \right)$ 为给定当前状态 s_t 和动作 a_t ，环境转移到状态 $s_{t+1}$ 的概率。

给定轨迹 $\tau$ ，累计奖励为 $R\left( \tau \right)=\sum_{t=1}^{T}{r_t}$ 。累计奖励称为回报（Return）。希望 Actor 在交互过程中回报总是尽可能多，但是回报并非是一个标量值，因为 Actor 采取哪一个动作 $p_{\theta}\left( a_t|s_t \right)$ 以及环境转移到哪一个状态 $p\left( s_{t+1}|s_t,a_t \right)$ 均以概率形式发生，因此轨迹 $\tau$ 和对应回报 $R\left( \tau \right)$ 均为随机变量，只能计算回报的期望：

$\bar{R}_{\theta}=\sum_{\tau}R\left( \tau \right)p_{\theta}\left( \tau \right)=\mathbb{E}_{\tau\sim p_{\theta}\left( \tau \right)}\left[ R\left( \tau \right) \right]\tag6$ 其中 $\bar{R}_{\theta}$ 表示使用参数为 $\theta$ 的策略与环境交互的期望回报，轨迹 $\tau$ 服从 $p_{\theta}\left( \tau \right)$ 的概率分布。

给定一条轨迹，回报总是固定的，因此只能调整策略函数参数 $\theta$ 使得高回报的轨迹发生概率尽可能大，而低回报的轨迹发生概率尽可能小。为了优化参数 $\theta$ ，可以使用梯度上升方法，优化 $\theta$ 使得期望回报 $\bar{R}_{\theta}$ 尽可能大： $\nabla\bar{R}_{\theta}=\sum_{\tau}R\left( \tau \right)\nabla p_{\theta}\left( \tau \right)\tag7$ 观察上式可以注意到，只有 $\nabla p_{\theta}\left( \tau \right)$ 与 $\theta$ 有关。考虑到 $p_{\theta}\left( \tau \right)$ 如公式 5 所示是多个概率值的连乘，难以进行梯度优化，因此将 $\nabla p_{\theta}\left( \tau \right)$ 转化为 $\nabla \text{log }p_{\theta}\left( \tau \right)$ 的形式使之易于计算。

根据 $\nabla p_{\theta}\left( \tau \right) = p_{\theta}\nabla \text{log }p_{\theta}\left( \tau \right)$ ，带入公式 7 可得： $\begin{align} \nabla\bar{R}_{\theta}&=\sum_{\tau}R\left( \tau \right)\nabla p_{\theta}\left( \tau \right) \\ &=\sum_{\tau}R\left( \tau \right) p_{\theta}\left( \tau \right) \nabla \text{log }p_{\theta}\left( \tau \right) \\ &=\mathbb{E}_{\tau \sim p_{\theta}\left( \tau \right)}\left[ R\left( \tau \right) \nabla \text{log }p_{\theta}\left( \tau \right) \right] \end{align} \tag8$ 在上式基础上，将公式 5 带入 $\nabla \text{log }p_{\theta}\left( \tau \right)$ ，可以继续推导得到：

$\begin{align} \nabla p_{\theta}\left( \tau \right) & =\nabla\left( \text{log }p\left( s_1 \right) +\sum_{t=1}^T \text{log }p_{\theta}\left( a_t|s_t \right)+\sum_{t=1}^T\text{log }p\left( s_{t+1|s_t,a_t} \right)\right) \\ &=\nabla \sum_{t=1}^T \text{log }p_{\theta}\left( a_t|s_t \right) \\ &=\sum_{t=1}^T \nabla \text{log }p_{\theta}\left( a_t|s_t \right) \end{align} \tag9$ 这里是对策略函数参数 $\theta$ 求梯度，而 $p\left( s_1 \right)$ 和 $p\left( s_{t+1}|a_t \right)$ 由环境决定，与策略函数参数 $\theta$ 无关，因此这两项的梯度为 0。将上式带入公式 8 可得： $\begin{align} \nabla\bar{R}_{\theta} &=\mathbb{E}_{\tau \sim p_{\theta}\left( \tau \right)}\left[ R\left( \tau \right) \nabla \text{log }p_{\theta}\left( \tau \right) \right]\\ &=\mathbb{E}_{\tau \sim p_{\theta}\left( \tau \right)}\left[ R\left( \tau \right) \sum_{t=1}^T\nabla \text{log }p_{\theta}\left( a_t|s_t \right) \right]\\ \end{align} \tag{10}$ 由于期望无法直接计算，因此在实践中，通常是从概率分布 $p_{\theta}\left( \tau \right)$ 中采样条轨迹近似计算期望：

$\begin{align} \nabla\bar{R}_{\theta} &=\mathbb{E}_{\tau \sim p_{\theta}\left( \tau \right)}\left[ R\left( \tau \right) \sum_{t=1}^T\nabla \text{log }p_{\theta}\left( a_t|s_t \right) \right]\\ &\approx \frac{1}{N}\sum_{n=1}^N R\left( \tau^n \right)\sum_{t=1}^{T_n}\nabla \text{log }p_{\theta}\left( a^{n}_t|s^n_t \right)\\ &=\frac{1}{N}\sum_{n=1}^N \sum_{t=1}^{T_n}R\left( \tau^n \right)\nabla \text{log }p_{\theta}\left( a^{n}_t|s^n_t \right) \end{align} \tag{11}$ 可以使用学习率为 $\eta$ 的梯度上升方法优化策略参数 $\theta$ ，使之能够获得更高的回报：

$\theta \leftarrow \theta+\eta\nabla\bar{R}_{\theta}\tag{12}$ 为了解决训练过程中的不稳定问题，通常会在回报 $R\left( \tau^n \right)$ 上减去一个基线（baseline），使得这一项的期望为 0，这样在实际更新的时候概率值更新会有正有负，最终概率更新幅度之和大致为 0。从而避免因为某些动作没有被采样而动作概率下降的问题。回报的梯度如下所示：

$\begin{align} \nabla\bar{R}_{\theta}\approx\frac{1}{N}\sum_{n=1}^N \sum_{t=1}^{T_n}\left( R\left( \tau^n \right)-b \right)\nabla \text{log }p_{\theta}\left( a^{n}_t|s^n_t \right) \end{align} \tag{13}$ 其中 $b=\mathbb{E}_{\tau \sim p_{\theta}\left( \tau \right)}R\left( \tau \right)$ ，即回报的期望。这一项在实践中常用的计算方法是，在训练过程中记录历史 $R\left( \tau^n \right)$ 的均值用以估计回报的期望。

公式 (13) 中仍然存在另外一个问题值得考虑， $\forall t\in\left[ 1,T \right],\nabla\text{log }p_{\theta}\left( a_t^n|s_t^n \right)$ 的权重始终为 $R\left( \tau^n \right)$ ，这意味着在一条轨迹中所有的动作都具有同样的价值。然而从直觉上来看，一条轨迹中一般不会所有的动作都是好的，而是有些动作好，而另外一些动作差，然而这些动作目前却会以相同的方式更新概率，这也会造成训练的不稳定。因此有必要为每个动作赋予其所应得的奖励。考虑到交互过程中 Actor 采取某一动作只会对之后的状态产生影响，而不会对之前的有影响。因此，不必令每个动作的权重都为全部奖励之和 $R\left( \tau^n \right)=\sum_{t'=1}^{T_n}r_{t'}^n$ ，而只需要累计在当前动作之后的奖励之和 $R\left( \tau^n \right)=\sum_{t'=t}^{T_n}r_{t'}^n$ 。

另一个直觉是，当前动作会对时间较近的状态影响大，时间较远的影响小。因此，在计算累计奖励的时候，对于未来较遥远的奖励应该予以折扣，即 $R\left( \tau^n \right)=\sum_{t'=t}^{T_n}\gamma^{t'-t} r_{t'}^n$ 。引入新的奖励之后，公式（13）中回报的梯度表示为：

$\begin{align} \nabla\bar{R}_{\theta}\approx\frac{1}{N}\sum_{n=1}^N \sum_{t=1}^{T_n}\left( \sum_{t'=t}^{T_n}\gamma^{t'-t} r_{t'}^n-b \right)\nabla \text{log }p_{\theta}\left( a^{n}_t|s^n_t \right) \end{align} \tag{14}$

公式（14）中的 $\sum_{t'=t}^{T_n}\gamma^{t'-t} r_{t'}^n$ 反应了给定状态 s_t^n 下采取动作 a_t^n 的收益，该收益称为动作价值（Action Value），并用 $Q\left( s,a \right)$ 表示。而 $b=\mathbb{E}_{a \sim p_{\theta}\left( a|s \right)}Q\left( s,a \right)$ 则是动作价值的期望。由于动作价值的期望与具体动作无关，因此这个期望也称为状态价值（State Value），并用 $V\left( s\right)$ 来表示。即：

$动作价值：Q\left( s,a \right)=\sum_{t'=t}^{T}\gamma^{t'-t} r_{t'}\tag{15}$ 将状态-动作 $\left( s,a\right)$ 的梯度权重抽象为 $Q\left( s,a \right)-V\left( s \right)$ 。给定状态下， $Q\left( s,a \right)$ 衡量了具体动作的价值，而 $V\left( s\right)$ 则表示 Actor 采取各种可能动作的期望价值。因此 $Q\left( s,a \right)-V\left( s \right)$ 可以理解为采取特定动作相比较于随机一个动作的优势（Advantage）。优势越大，说明采取动作要比其他可能动作更好，使用 $A\left( s,a \right)=Q\left( s,a \right)-V\left( s \right)$ 来表示优势函数。

根据前面公式（10）和公式（12），策略梯度的基本形式如下：

$\begin{align} \nabla\bar{R}_{\theta} &=\mathbb{E}_{\tau \sim p_{\theta}\left( \tau \right)}\left[ R\left( \tau \right) \nabla \text{log }p_{\theta}\left( \tau \right) \right] \end{align} \tag{16}$

$\theta \leftarrow \theta+\eta\nabla\bar{R}_{\theta}\tag{17}$ 实际计算时，需要从环境中采样很多轨迹 $\tau$ ，然后按照上述策略梯度公式对策略函数参数 $\theta$ 进行更新。但是由于 $\tau$ 是从概率分布 $p_{\theta}\left( \tau \right)$ 中采样得到，一旦策略函数参数 $\theta$ 更新，那么概率分布 $p_{\theta}\left( \tau \right)$ 就会发生变化，因而之前采样过的轨迹便不能再次利用。所以策略梯度方法需要在不断地与环境交互中学习而不能利用历史数据。因而这种方法的训练效率低下。

策略梯度方法中，负责与环境交互的 Actor 与负责学习的 Actor 相同，这种训练方法被称为 On-Policy 训练方法。相反，Off-Policy 训练方法则将这两个 Actor 分离，固定一个 Actor 与环境交互而不更新它，而将交互得到的轨迹交由另外一个负责学习的 Actor 训练。Off-Policy 的优势是可以重复利用历史数据，从而提升训练效率。近端策略优化（Proximal Policy Optimization，PPO）就是 Off-Policy。

假设负责学习的智能体策略为 $\pi_{\theta}$ ，负责采样的智能体策略为 $\pi_{\theta'}$ 。按照公式（16）计算 $\mathbb{E}_{\tau \sim p_{\theta}\left( \tau \right)}\left[ R\left( \tau \right) \nabla \text{log }p_{\theta}\left( \tau \right) \right]$ ，但由于 Off-Policy，不能从 $p_{\theta}\left( \tau \right)$ 中采样得到 $\tau$ ，只能从 $p_{\theta'}$ 中采样，因此可以对公式（16）进行修正：

$\begin{align} \nabla\bar{R}_{\theta} &=\mathbb{E}_{\tau \sim p_{\theta'}\left( \tau \right)}\left[ \frac{p_{\theta}\left( \tau \right)}{p_{\theta'}\left( \tau \right)}R\left( \tau \right) \nabla \text{log }p_{\theta}\left( \tau \right) \right] \end{align} \tag{18}$ 回到前面讲的策略梯度的具体定义，如公式（14），并结合优势函数 $A^{\theta}\left( s_t,a_t \right)$ ，可以将公式（14）策略梯度的计算改为如下形式： $\begin{align} \nabla\bar{R}_{\theta} &=\mathbb{E}_{\left( s_t,a_t \right)\sim\pi_{\theta}}\left[ A^{\theta}\left( s_t,a_t \right)\nabla \text{log }p_{\theta}\left( a_t|s_t \right) \right] \end{align} \tag{19}$ 结合公式（18），将其改写为如下形式： $\begin{align} \nabla\bar{R}_{\theta} &=\mathbb{E}_{\left( s_t,a_t \right)\sim\pi_{\theta'}}\left[ \frac{p_{\theta}\left( s_t,a_t \right)}{p_{\theta'}\left( s_t,a_t \right)}A^{\theta'}\left( s_t,a_t \right)\nabla \text{log }p_{\theta}\left( a_t|s_t \right) \right] \end{align} \tag{20}$ 此时优势函数从 $A^{\theta}\left( s_t,a_t \right)$ 变成 $A^{\theta’}\left( s_t,a_t \right)$ ，采样策略也从 $\pi_{\theta}$ 变成 $\pi_{\theta'}$ 。

由于： $\begin{align} p_{\theta}\left( s_t,a_t \right)&=p_{\theta}\left( a_t|s_t \right)p_{\theta}\left( s_t \right)\\ p_{\theta'}\left( s_t,a_t \right)&=p_{\theta'}\left( a_t|s_t \right)p_{\theta'}\left( s_t \right) \end{align} \tag{21}$ 假设状态只与环境有关，与具体策略无关，那么 $p_{\theta}\left( s_t \right)\approx p_{\theta'}\left( s_t \right)$ ，那么公式（20）可以改写为：

$\begin{align} \nabla\bar{R}_{\theta} &=\mathbb{E}_{\left( s_t,a_t \right)\sim\pi_{\theta'}}\left[ \frac{p_{\theta}\left( s_t|a_t \right)}{p_{\theta'}\left( s_t|a_t \right)}A^{\theta'}\left( s_t,a_t \right)\nabla \text{log }p_{\theta}\left( a_t|s_t \right) \right] \end{align} \tag{22}$ 从上述式子的梯度形式反推原来的目标函数，可以得到如下公式：

$\begin{align} J^{\theta'}\left( \theta \right) &=\mathbb{E}_{\left( s_t,a_t \right)\sim\pi_{\theta'}}\left[ \frac{p_{\theta}\left( s_t|a_t \right)}{p_{\theta'}\left( s_t|a_t \right)}A^{\theta'}\left( s_t,a_t \right)\right] \end{align} \tag{22}$ 其中， $J^{\theta'}\left( \theta \right)$ 表示需要优化的目标函数。

为了保证分布 $p_{\theta}$ 和 $p_{\theta'}$ 不要相差太多，PPO 使用KL 散度来约束 $\theta$ 和 $\theta'$ ，使之更加相似，表示如下：

$\begin{align} J^{\theta'}\left( \theta \right)_{\text{PPO}}&= J^{\theta'}\left( \theta \right)-\beta\text{ KL}\left( \pi_{\theta},\pi_{\theta'} \right)\\ J^{\theta'}\left( \theta \right) &=\mathbb{E}_{\left( s_t,a_t \right)\sim\pi_{\theta'}}\left[ \frac{p_{\theta}\left( s_t|a_t \right)}{p_{\theta'}\left( s_t|a_t \right)}A^{\theta'}\left( s_t,a_t \right)\right] \end{align} \tag{23}$ 公式（23）就是 PPO 最终的优化目标。

DPO

前面我们详细介绍了 RLHF 的原理，整个过程略显复杂。首先需要训练好 Reward Model，然后在 PPO 阶段需要加载 4 个模型：Actor Model 、Reward Mode、Critic Model 和 Reference Model。对计算资源要求极高，而且训练时间长，对于一般人来说很难玩得起。

好在 2023 年 5 月，斯坦福大学提出了 PPO 的简化版：DPO（Direct Preference Optimization）。只需要加载 2 个模型，而且不需要在线采样数据，极大地节省了训练开销。下图的右边是 DPO 的训练流程：

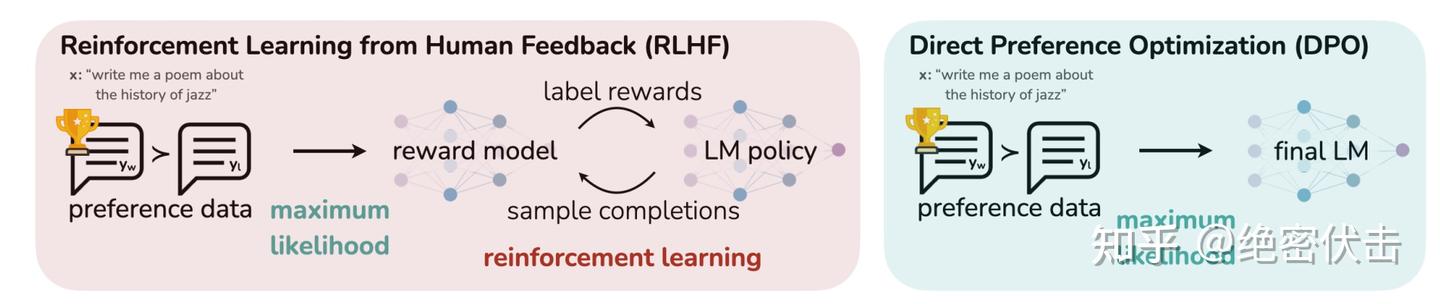图 7：PPO 和 DPO 的区别

下面就简单介绍下 DPO 是如何简化 PPO 的。

首先回顾一下前面讲的 RLHF 是怎么训练的：

第一步是训练 Reward Model。训练数据是同一个 prompt 的 2 个回答，让人或 GPT-4o 标注哪个回答更好，Reward Model 会去优化如下目标：

$\mathcal{L}_{R}\left( r_{\phi},\mathcal{D} \right)=-\mathbb{E}_{(x,y_\text{win},y_\text{lose})\sim\mathcal{D}}[\log\sigma(r_\phi(x,y_\text{win})-r_\phi(x,y_\text{lose}))]\tag{24}$

其中 $r_\phi$ 就是 Reward Model 用来给回答打分。 $\mathcal{D}$ 是训练数据集，是 prompt， $y_\text{win}$ 和 $y_\text{lose}$ 分别是好的回答和不好的回答。也就是说，要尽可能让好的回答的得分比不好的回答高，拉大他们之间的差别。

第二步是用 RL 算法来提升模型的得分。优化的目标是：

$\max_{\pi_\theta}\left\{\mathbb{E}_{x\sim \mathcal{D},y\sim\pi_\theta(y|x)}[r_\phi(x,y)]-\beta\mathbb{D}_{\text{KL}}[\pi_\theta(y|x)||\pi_\text{ref}(y|x)]\right\}\tag{25}$

其中 $\pi_\theta$ 是我们需要训练的 LLM， $\pi_\text{ref}$ 是 Reference Model。这个优化目标的是希望 LLM 输出的回答的评分能尽可能高，同时 $\pi_\theta$ 不要偏离 $\pi_\text{ref}$ 太多。

DPO 的作者们意识到，后面的这个式子是有显式解的。因为：

$\begin{aligned}\max_{\pi_\theta}&\left\{\mathbb{E}_{x\sim \mathcal{D},y\sim\pi_\theta(y|x)}[r_\phi(x,y)] -\beta\mathbb{D}_{\text{KL}}[\pi_\theta(y|x)||\pi_\text{ref}(y|x)]\right\}\\&=\max_{\pi_\theta}\mathbb{E}_{x\sim \mathcal{D},y\sim\pi_\theta(y|x)}[r_\phi(x,y) - \beta \log \frac{\pi_\theta(y|x)}{\pi_\text{ref}(y|x)}]\\&=\min_{\pi_\theta}\mathbb{E}_{x\sim \mathcal{D},y\sim\pi_\theta(y|x)}[\log \frac{\pi_\theta(y|x)}{\pi_\text{ref}(y|x)} - \frac{1}{\beta} r_\phi(x,y)]\\&=\min_{\pi_\theta}\mathbb{E}_{x\sim \mathcal{D},y\sim\pi_\theta(y|x)}[\log\frac{\pi_\theta(y|x)}{\pi_\text{ref}(y|x)e^{r_\phi(x,y)/\beta}}]\end{aligned}\tag{26}$

如果我们归一化一下分母，即取 $Z(x)=\sum_y\pi_\text{ref}(y|x)e^{r_\phi(x,y)/\beta}$ ，也就可以构造出一个新的概率分布：

$\pi^*(y|x) = \pi_\text{ref}(y|x)e^{r_\phi(x,y)/\beta}/Z(x)\tag{27}$

那么上式变成了：

$\begin{aligned}\min_{\pi_\theta}&\mathbb{E}_{x\sim \mathcal{D},y\sim\pi_\theta(y|x)}[\log\frac{\pi_\theta(y|x)}{\pi_\text{ref}(y|x)e^{r_\phi(x,y)/\beta}}]\\ &=\min_{\pi_\theta}\mathbb{E}_{x\sim \mathcal{D},y\sim\pi_\theta(y|x)}[\log\frac{\pi_\theta(y|x)}{\pi^*(y|x)}-\log Z(x)]\\ &=\min_{\pi_\theta}\mathbb{E}_{x\sim \mathcal{D},y\sim\pi_\theta(y|x)}[\log\frac{\pi_\theta(y|x)}{\pi^*(y|x)}]\\ &=\min_{\pi_\theta}\mathbb{E}_{x\sim \mathcal{D}}\mathbb{D}_\text{KL}(\pi_\theta(y|x)||\pi^*(y|x)) \end{aligned}\tag{28}$

由于 KL 散度在 2 个分布相等时取最小值，我们得到了这样的结论：RLHF 训练希望得到的最优的概率分布就是 $\pi^*$ 。

另一个角度来说，由 $\pi^*$ 的公式，我们相当于是得到了 $r_\phi$ 和 $\pi^*$ 的关系，那么是否我们可以把训练 $r_\phi$ 转化成直接去训练 $\pi^*$ 呢？

简单转换一下 $\pi^*$ 的定义式，可以得到：

$r_{\phi}(x,y)=\beta\log\frac{\pi^*(y|x)}{\pi_\text{ref}(y|x)}+\beta \log Z(x)\tag{29}$

带入公式（25），也就有了：

$\max_{\pi^*}\left\{\mathbb{E}_{(x,y_\text{win},y_\text{lose})\sim\mathcal{D}}[\log\sigma(\beta\log\frac{\pi^*(y_\text{win}|x)}{\pi_\text{ref}(y_\text{win}|x)} - \beta\log\frac{\pi^*(y_\text{lose}|x)}{\pi_\text{ref}(y_\text{lose}|x)})]\right\}\tag{30}$

同样的，我们可以直接用这个优化目标去求 $\pi_\theta$ ：

$\max_{\pi_\theta}\left\{\mathbb{E}_{(x,y_\text{win},y_\text{lose})\sim\mathcal{D}}[\log\sigma(\beta\log\frac{\pi_\theta(y_\text{win}|x)}{\pi_\text{ref}(y_\text{win}|x)} - \beta\log\frac{\pi_\theta(y_\text{lose}|x)}{\pi_\text{ref}(y_\text{lose}|x)})]\right\}\tag{31}$

最终，我们可以得出 DPO 的 loss 如下所示： $\mathcal{L}_{\text{DPO}}\left( \pi_{\theta};\pi_{\text{ref}} \right)=-\mathbb{E}_{(x,y_\text{win},y_\text{lose})\sim\mathcal{D}}[\log\sigma(\beta\log\frac{\pi_\theta(y_\text{win}|x)}{\pi_\text{ref}(y_\text{win}|x)} - \beta\log\frac{\pi_\theta(y_\text{lose}|x)}{\pi_\text{ref}(y_\text{lose}|x)})]\tag{31}$ 这就是 DPO 的 loss。DPO 通过以上的公式转换把 RLHF 巧妙地转化为了 SFT，在训练的时候不再需要同时跑 4 个模型（Actor Model 、Reward Mode、Critic Model 和 Reference Model），而是只用跑 Actor 和 Reference 2 个模型。

DPO 变种

DPO 出来之后，由于其简单易用的特点，迅速成为大模型训练的标配，随后也出现了各种变种，比如 SimPO、Step-DPO、MCTS-DPO、SPO、Iterative-DPO。下面就以 Iterative-DPO 为例，介绍一下做了哪些改动。

Iterative-DPO

Iterative Reasoning Preference Optimization 是 2024 年 Meta 提出的 DPO 改进版。

思路很简单，下面介绍下具体流程：

首先训练一个 Reward Model。然后将训练数据分成 m 等份（比如 3 等份），取第一份数据，用 LLM 对每个 prompt 采样出 k 个答案，使用 Reward Model 对 k 个回答进行打分，选出得分最高的和最低的，构建成 pair 对。使用第一份 pair 对数据训练一轮 DPO，更新 LLM。再取第二份数据，用更新后的 LLM 对第二份数据的每个 prompt 采样出 k 个答案，使用 Reward Model 对 k 个回答进行打分，选出得分最高的和最低的，构建成 pair 对。使用第二份 pair 对数据在更新后的 LLM 上训练一轮 DPO。重复以上过程，直到 m 份数据全部训练完成。

下图是 Iterative-DPO 的具体流程：

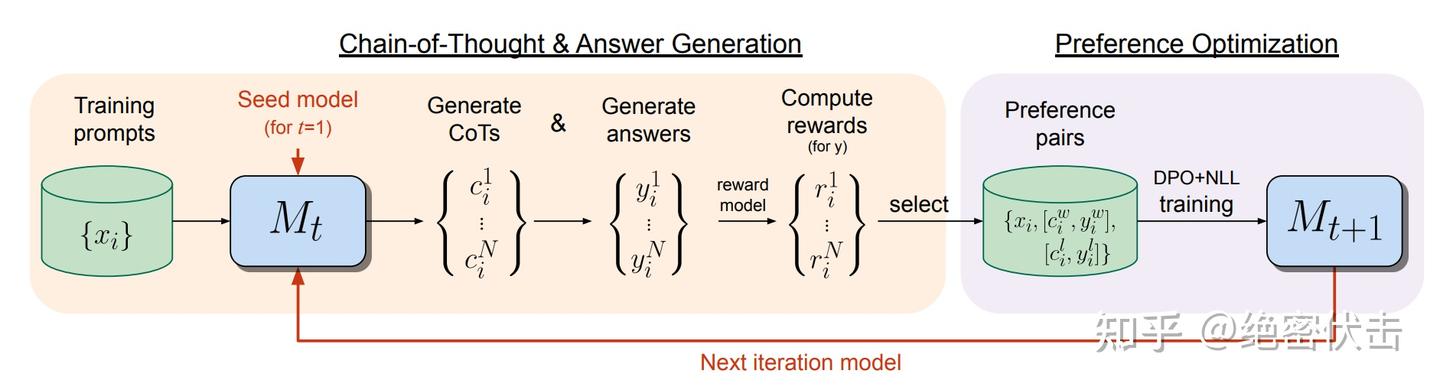图 7：Iterative-DPO 流程

由于 Iterative DPO 在每轮训练完成后，都会基于最新模型重新采样数据，构建 pair 对，因此 Iterative DPO 是介于 Online-Policy 和 Offline-Policy 之间。

下图是 Iterative DPO 的两阶段流程：

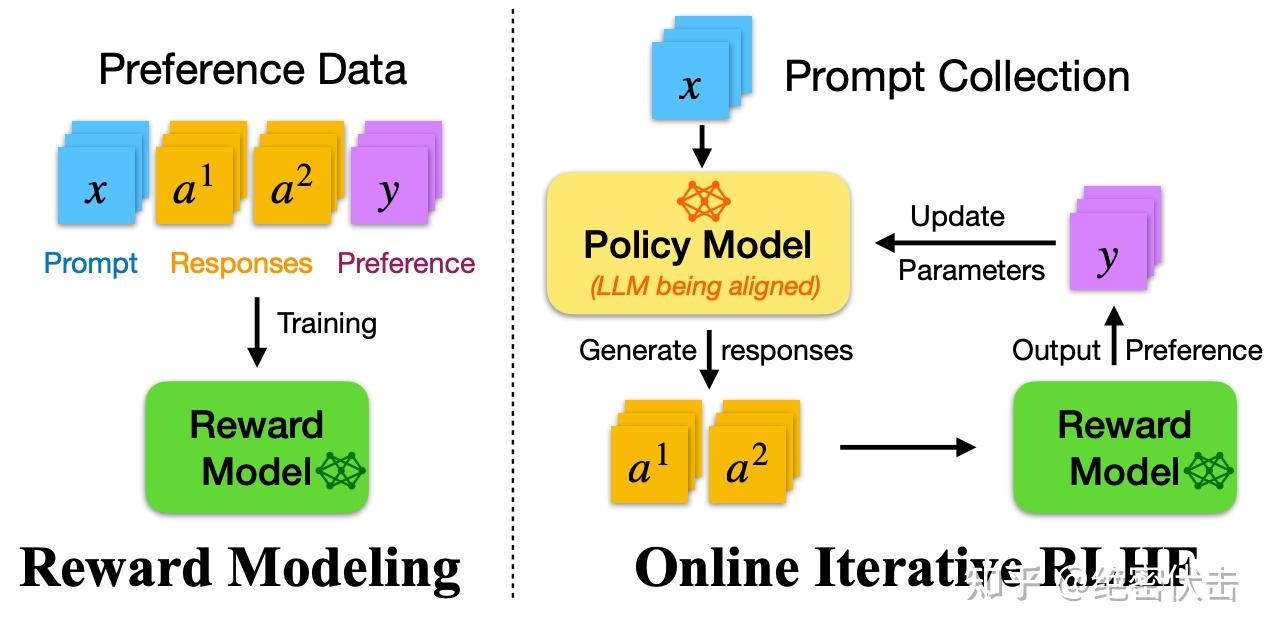图 8： Iterative DPO 两阶段流程总结

现今，强化学习已成为大型模型的标配技术，特别是随着 OpenAI O1 的发布，该技术作为其核心方法，掌握并熟练运用强化学习已成为不可或缺的技能。本文简要概述了 RLHF 的基础知识，并初步介绍了 PPO 和 DPO，待日后有机会，将进一步深入学习 PPO 的其他变体。

参考

DeepSpeed-Chat: Easy, Fast and Affordable RLHF Training of ChatGPT-like Models at All Scales

Secrets of RLHF in Large Language Models Part I: PPO

Direct Preference Optimization: Your Language Model is Secretly a Reward Model

Proximal Policy Optimization Algorithms

朱小霖：DPO 是如何简化 RLHF 的

infgrad：DPO: Direct Preference Optimization 论文解读及代码实践

RLHF Workflow: From Reward Modeling to Online RLHF

书籍：《大规模语言模型——从原理到实践》

大疆无人机经纬m600pro开箱 大模型优化利器：RLHF之PPO、DPO

大疆无人机经纬m600pro开箱大模型优化利器：RLHF之PPO、DPO