高斯混合模型（Gaussian Mixed Model, GMM）指的是多个高斯分布函数的线性组合，理论上GMM可以拟合出任意类型的分布，通常用于解决同一集合下的数据包含多个不同的分布的情况（或者是同一类分布但参数不一样，或者是不同类型的分布，比如正态分布和伯努利分布）。
GMM可用于各种机器学习应用，包括聚类、密度估计和模式识别。
高斯混合模型是一种常见的混合模型。设有随机变量 X X X，则GMM的概率密度由高斯分布的混合给出:：
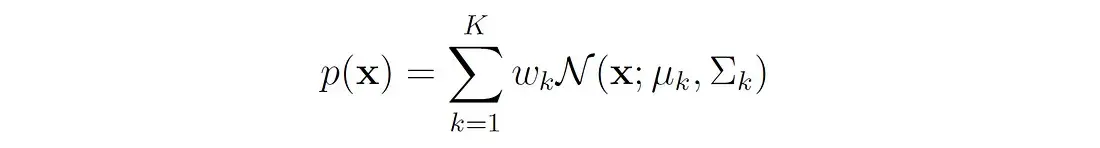
其中：
k代表该分布由 k 个高斯分量组成 w k w_k wk 就是每个分量 N ( x ∣ μ k , Σ k ) N ( x ∣ μ_k , Σ_k ) N(x∣μk,Σk) 的权重 μ k μ_k μk是第k个高斯分量的平均向量 Σ k Σ_k Σk是第k个高斯分量的协方差矩阵 N ( x ∣ μ k , Σ k ) N ( x ∣ μ_k , Σ_k ) N(x∣μk,Σk)为第k个分量的多元正态密度函数 二、GMM参数估计GMM常用于聚类。如果要从 GMM 的分布中随机地取一个点的话，实际上可以分为两步：
首先随机地在这 K 个 Component 之中选一个，每个 Component 被选中的概率实际上就是它的系数 w k w_k wk选中 Component 之后，再单独地考虑从这个 Component 的分布中选取一个点就可以了──这里已经回到了普通的 Gaussian 分布，转化为已知的问题。将GMM用于聚类时，假设数据服从混合高斯分布（Mixture Gaussian Distribution），那么只要根据数据推出 GMM 的概率分布来就可以了；然后 GMM 的 K 个 Component 实际上对应 K个 cluster 。根据数据来推算概率密度通常被称作 density estimation 。特别地，当我已知（或假定）概率密度函数的形式，而要估计其中的参数的过程被称作『参数估计』。
对于具有K个分量的GMM，数据集为
X
=
X
1
,
…
,
X
n
X = {X_1,…,X_n}
X=X1,…,Xn (n个数据点)，似然函数L由每个数据点的概率密度乘积给出，由GMM定义: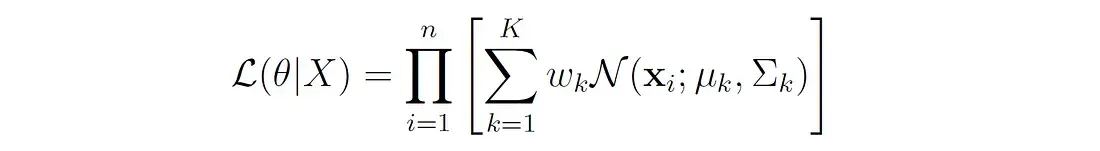 
其中，
θ
θ
θ表示模型的所有参数(均值、方差和混合权重)。
在实际应用中，使用对数似然更容易，因为概率的乘积可能导致大型数据集的数值下溢。对数似然由下式给出: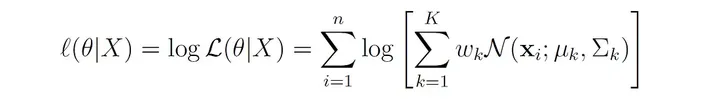 
GMM的参数可以通过对 θ θ θ最大化对数似然函数来估计。但是我们不能直接应用极大似然估计(MLE)来估计GMM的参数，这是因为:
对数似然函数是高度非线性的，难于解析最大化。该模型具有潜在变量(混合权重)，这些变量在数据中不能直接观察到。为了克服这些问题，通常使用 期望最大化(EM)算法 来解决这个问题。
三、期望最大化（EM）算法EM算法是在依赖于未观察到的潜在变量的统计模型中寻找参数的最大似然估计的有力方法。该算法首先随机初始化模型参数。然后在两个步骤之间迭代:
期望步(E步)：根据观察到的数据和模型参数的当前估计，计算模型相对于潜在变量分布的期望对数似然。这一步包括对潜在变量的概率进行估计。最大化步(M步)：更新模型的参数，以最大化观察数据的对数似然，给定E步骤估计的潜在变量。这两个步骤重复直到收敛，通常由对数似然变化的阈值或迭代的最大次数决定。
在GMM中，潜在变量表示每个数据点的未知分量隶属度。设Z为随机变量，表示生成数据点x的分量。Z可以取值 1 , … , K {1,…,K} 1,…,K 中的一个，对应于K个分量。
3.1 E-Step在E步中，我们根据模型参数的当前估计值计算潜在变量Z的概率分布。换句话说，我们计算每个高斯分量中每个数据点的隶属度概率。
Z= k的概率，即x属于第k个分量，可以用贝叶斯规则计算:
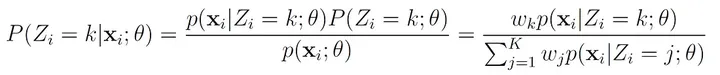
我们用变量 γ ( z k ) γ(z_k) γ(zk)来表示这个概率，可以这样写:
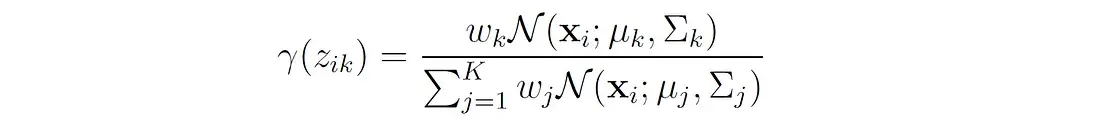
变量 γ ( z k ) γ(z_k) γ(zk)通常被称为responsibilities，因为它们描述了每个分量对每个观测值的responsibilities。这些参数作为关于潜在变量的缺失信息的代理。
关于潜在变量Z分布的期望对数似然现在可以写成:
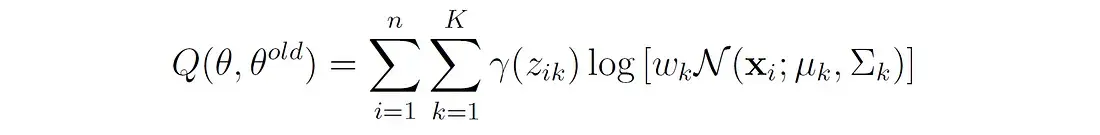
函数Q是每个高斯分量下所有数据点的对数似然的加权和，权重就是我们上面说的responsibilities。Q不同于前面显示的对数似然函数l(θ|X)。对数似然l(θ|X)表示整个混合模型下观测数据的似然，没有明确考虑潜在变量，而Q表示观测数据和估计潜在变量分布的期望对数似然。
3.2 M-Step在M步中，更新GMM的参数 θ θ θ(均值、协方差和混合权值)，以便使用E步中计算的最大化期望似然 Q ( θ ) Q(θ) Q(θ)。
参数更新如下:
更新每个分量的方法: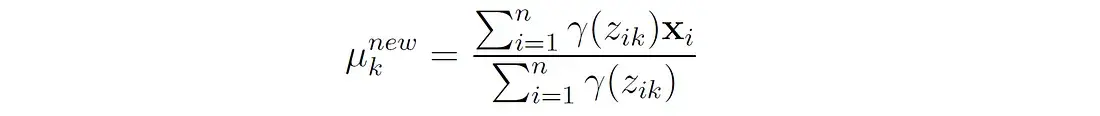
第k个分量的新平均值是所有数据点的加权平均值，权重是这些点属于分量k的概率。这个更新公式可以通过最大化期望对数似然函数Q相对于平均值 μ k μ_k μk而得到。
以下是证明步骤，单变量高斯分布的期望对数似然为： 
这个函数对
μ
k
μ_k
μk求导并设其为0，得到: 
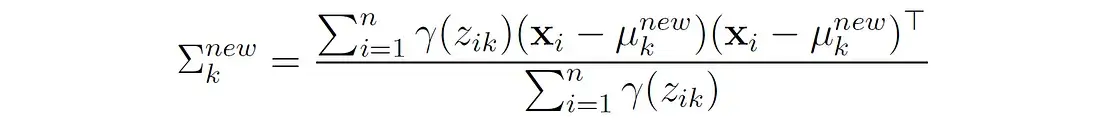也就是说，第k个分量的新协方差是每个数据点与该分量均值的平方偏差的加权平均值，其中权重是分配给该分量的点的概率。
在单变量正态分布的情况下，此更新简化为: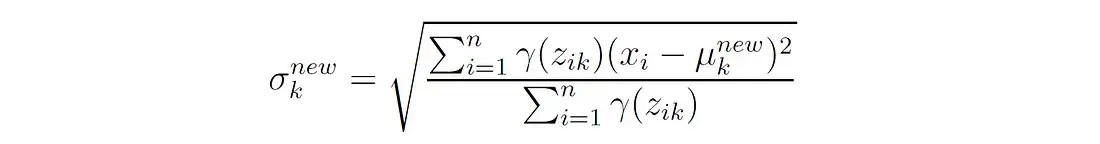 
3. 更新混合权值
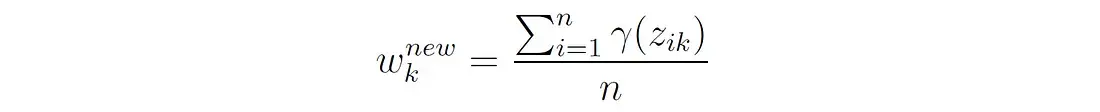也就是说，第k个分量的新权重是属于该分量的点的总概率，用n个点的个数归一化。
重复这两步保证收敛到似然函数的局部最大值。由于最终达到的最优取决于初始随机参数值，因此通常的做法是使用不同的随机初始化多次运行EM算法，并保留获得最高似然的模型。
四、GMM的Python实现下面将使用Python实现EM算法，用于从给定数据集估计两个单变量高斯分布的GMM的参数。
首先导入所需的库:
import numpy as np import matplotlib.pyplot as plt import seaborn as sns from scipy.stats import norm np.random.seed(0) # for reproducibility接下来，让我们编写一个函数来初始化GMM的参数:
def init_params(x): """Initialize the parameters for the GMM """ # Randomly initialize the means to points from the dataset mean1, mean2 = np.random.choice(x, 2, replace=False) # Initialize the standard deviations to 1 std1, std2 = 1, 1 # Initialize the mixing weights uniformly w1, w2 = 0.5, 0.5 return mean1, mean2, std1, std2, w1, w2均值从数据集中的随机数据点初始化，标准差设为1，混合权重设为0.5。
E步，计算属于每个高斯分量的每个数据点的概率:
def e_step(x, mean1, std1, mean2, std2, w1, w2): """E-Step: Compute the responsibilities """ # Compute the densities of the points under the two normal distributions prob1 = norm(mean1, std1).pdf(x) * w1 prob2 = norm(mean2, std2).pdf(x) * w2 # Normalize the probabilities prob_sum = prob1 + prob2 prob1 /= prob_sum prob2 /= prob_sum return prob1, prob2M步，根据e步计算来更新模型参数:
def m_step(x, prob1, prob2): """M-Step: Update the GMM parameters """ # Update means mean1 = np.dot(prob1, x) / np.sum(prob1) mean2 = np.dot(prob2, x) / np.sum(prob2) # Update standard deviations std1 = np.sqrt(np.dot(prob1, (x - mean1)**2) / np.sum(prob1)) std2 = np.sqrt(np.dot(prob2, (x - mean2)**2) / np.sum(prob2)) # Update mixing weights w1 = np.sum(prob1) / len(x) w2 = 1 - w1 return mean1, std1, mean2, std2, w1, w2最后编写运行EM算法的主函数，在E步和M步之间迭代指定次数的迭代:
def gmm_em(x, max_iter=100): """Gaussian mixture model estimation using Expectation-Maximization """ mean1, mean2, std1, std2, w1, w2 = init_params(x) for i in range(max_iter): print(f'Iteration {i}: μ1 = {mean1:.3f}, σ1 = {std1:.3f}, μ2 = {mean2:.3f}, σ2 = {std2:.3f}, ' f'w1 = {w1:.3f}, w2 = {w2:.3f}') prob1, prob2 = e_step(x, mean1, std1, mean2, std2, w1, w2) mean1, std1, mean2, std2, w1, w2 = m_step(x, prob1, prob2) return mean1, std1, mean2, std2, w1, w2为了测试我们的实现，需要将通过从具有预定义参数的已知混合分布中采样数据来创建一个合成数据集。然后将使用EM算法估计分布的参数，并将估计的参数与原始参数进行比较。
首先从两个单变量正态分布的混合物中采样数据:
def sample_data(mean1, std1, mean2, std2, w1, w2, n_samples): """Sample random data from a mixture of two Gaussian distribution. """ x = np.zeros(n_samples) for i in range(n_samples): # Choose distribution based on mixing weights if np.random.rand()