买华为手机选什么系列的好用 Bubble Sort Algorithm

Bubble Sort

Bubble Sort is one of the simplest sorting algorithms. It repeatedly steps through the list, compares adjacent elements, and swaps them if they are in the wrong order. This process is repeated until the list is sorted.

Although Bubble Sort is easy to understand and implement, it is not the most efficient sorting algorithm, especially for large datasets, as its time complexity is \(O(n^2)\) in the worst and erage cases.

Algorithm

Here are the steps of the Bubble Sort algorithm:

Start from the first element of the array. Compare the current element with the next element. If the current element is greater than the next element, swap them. Move to the next element and repeat steps 2 and 3 until the end of the array. Repeat steps 1 to 4 for all elements, reducing the range of comparison each time, as the largest elements are placed at the end of the array after each iteration. Stop when no swaps are needed, indicating that the array is sorted. Example for Bubble Sort

Let’s sort the array [5, 3, 8, 4, 2] using Bubble Sort and explain each step:

Initial Array: Pass 1:

Compare and swap adjacent elements if needed:

Compare 5 and 3Swap since 5 > 3 Compare 5 and 8No swap needed. Compare 8 and 4Swap since 8 > 4 Compare 8 and 2Swap since 8 > 2

The largest element (8) is now at the end.

Pass 2:

Compare and swap adjacent elements in the reduced range:

Compare 3 and 5No swap needed Compare 5 and 4Swap since 5 > 4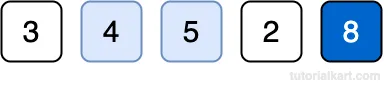 Compare 5 and 2Swap since 5 > 2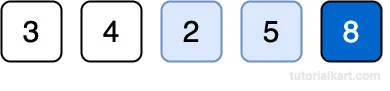

The second largest element (5) is now in its correct position.

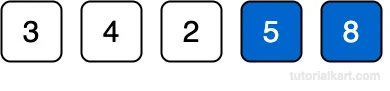Pass 3:

Compare and swap adjacent elements in the further reduced range:

Compare 3 and 4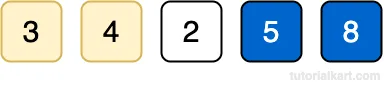No swap needed. Compare 4 and 2Swap since 4 > 2

The third largest element (4) is now in its correct position.

Pass 4:

Compare the remaining unsorted elements:

Compare 3 and 2Swap since 3 > 2

Now, all elements are sorted.

Final Sorted Array: Complexity of Bubble Sort

The time and space complexity of the Bubble Sort algorithm can be analyzed as follows:

1 Time Complexity:

The time complexity of Bubble sort for an array can vary based on the order of items in a given input array.

Worst-Case Complexity (\(O(n^2)\)):

This occurs when the array is sorted in reverse order. For each element, the algorithm must compare it with every other element, leading to \(n-1 + n-2 + \dots + 1 = \dfrac{n(n-1)}{2}\) comparisons.

Average-Case Complexity (\(O(n^2)\)):

On erage, Bubble Sort will require half as many swaps as in the worst case, but the number of comparisons remains \(O(n^2)\).

Best-Case Complexity (\(O(n)\)):

If the array is already sorted, the algorithm only needs to trerse the array once to confirm it is sorted, making a total of \(n-1\) comparisons and no swaps.

2 Space Complexity:

Bubble Sort is an in-place algorithm, meaning it does not require additional space for another array. Thus, its space complexity is \(O(1)\), as it only requires a constant amount of extra memory for swapping elements.

3 Stability:

Bubble Sort is a stable sorting algorithm. This means that if two elements he the same value, their relative order will remain the same after sorting.

Summary of Time and Space Complexities for Bubble Sort CaseTime ComplexitySpace ComplexityWorst CaseO(n²)O(1)Average CaseO(n²)O(1)Best CaseO(n)O(1)Time and Space Complexity of Bubble Sort Algorithm Bubble Sort Programs in Different Programming Languages 1 Go Program for Bubble Sort

Reference: Bubble Sort Program in Go

Program – bubble_sort.go Copy package main import "fmt" // Function to implement Bubble Sort func bubbleSort(arr []int) { n := len(arr) for i := 0; i < n-1; i++ { swapped := false for j := 0; j < n-i-1; j++ { if arr[j] > arr[j+1] { // Swap elements arr[j], arr[j+1] = arr[j+1], arr[j] swapped = true } } // If no swaps were made, the list is already sorted if !swapped { break } } } func main() { // Input array arr := []int{64, 34, 25, 12, 22, 11, 90} // Display the original array fmt.Println("Original array:", arr) // Sort the array using Bubble Sort bubbleSort(arr) // Display the sorted array fmt.Println("Sorted array:", arr) } Output

Conclusion

Bubble Sort is easy to implement and works well for small datasets. However, for larger datasets, more efficient algorithms like Quick Sort or Merge Sort are recommended.